République
Française
Le patrimoine immobilier des personnes physiques
Un éclairage inédit à partir des données foncières
Cette rubrique reprend l’ensemble des éléments qui permettent de construire le modèle de prix implémenté dans le cadre du travail de thèse. Il repose sur les données DV3F, et utilise les modèles additifs généralisés (GAM) pour introduire les coordonnées spatiales.
Le modèle de prix se base sur les données DV3F à propos des ventes de logements uniques en France métropolitaine, avec un travail spécifique sur les valeurs aberrantes. Ces données permettent de calibrer la modélisation des prix, exploitant les modèles additifs généralisés (GAM dans la suite). Plusieurs méthodes alternatives ont été testées, méthode des moindres carrés (OLS), régression géographiquement pondérée (GWR) notamment. Le GAM est l'option qui minimise l’erreur moyenne. Des méthodes alternatives telles que random forest ou catboost n’ont pas été étudiées du fait de notre souhait de conserver un modèle transparent. Ce modèle calibré permet ensuite d’estimer la valeur de marché pour les logements présents dans les Fichiers Fonciers. Faute de données disponibles en Alsace et Moselle dans DV3F, ces territoires sont exclus de l'estimation.
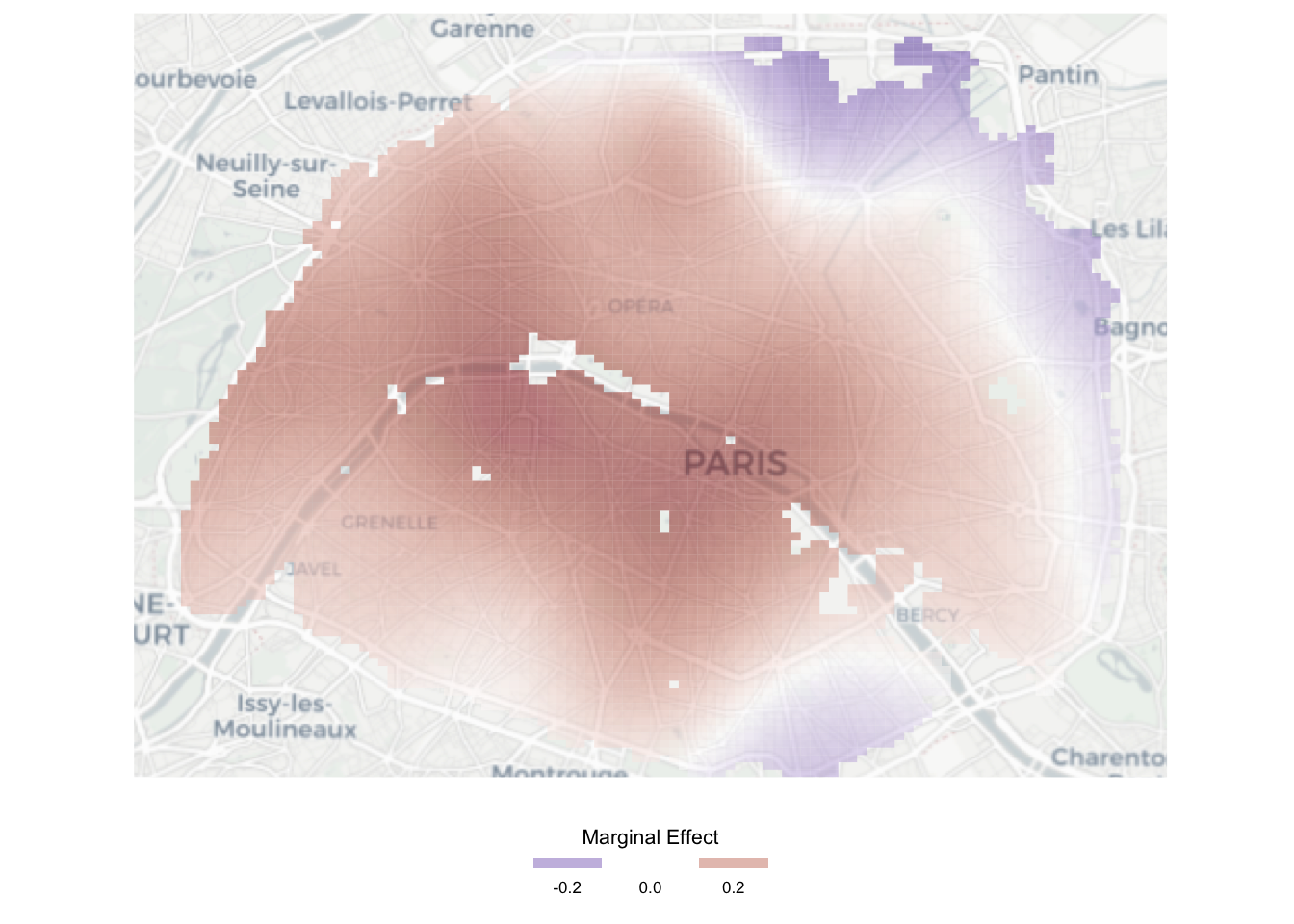
L’estimation est réalisée sur le premier trimestre de chaque année. Elle est menée au niveau de la zone d’emploi, maille homogène pour l’analyse des marchés immobiliers.
Dans un premier temps, nous détaillons les filtres imposés pour la base DV3F, puis détaillons l’implémentation ainsi que son principe général. Enfin, nous détaillons les paramètres retenus pour calibrer le modèle.
Les filtres sur la bases DV3F sont nombreux et ont pour principal objectif de supprimer les observations aberrantes, non pertinentes, ou avec des variables manquantes. L’objectif est de réduire en amont l’influence de ces observations dans la qualité de l’estimation.
Les principaux filtres appliqués à DV3F sont au nombre de quatre et concerne le type de transaction, le type de logement, le nombre de locaux associés à la mutation et les observations présentant des informations manquantes.
Une fois les premiers filtres appliqués, nous appliquons une seconde phase de filtrage afin de supprimer les valeurs aberrantes. Toutefois, comme cette notion se définit au niveau local (un bien à 9 000 euros par mètre carré est une valeur aberrante en zone détendue mais pas à Paris), nous choisissons d’appliquer la détection de ces valeurs aberrantes au niveau local. De fait, nous choisissons de supprimer les observations qui ne respectent pas les règles issues de l’IQR (suppression des observations inférieures au premier quartile moins 1,5 fois l'intervalle interquartile et supérieures au troisième quartile plus 1,5 fois l'intervalle interquartile).
Pour les municipalités avec peu d’observations, la méthode ne supprime pas d’observations. Concernant les municipalités avec de nombreuses informations, la méthode supprime uniquement les observations aberrantes, que ce soit par excès ou par défaut.
Enfin, les derniers filtres appliqués lors de la modélisation sont menés au niveau national : nous ne retenons que les opérations qui sont supérieures à 50 k€, et inférieures à 10 M€. Ainsi, on s’assure une cohérence grande, avec une réduction des valeurs potentiellement aberrantes.
L’implémentation du GAM sur les données disponibles est assez simple, car nous retenons comme variables explicatives le prix au mètre carré (choisi pour avoir une plus grande cohérence), la surface du bien, la surface des dépendances associées, ainsi que l’âge du bâti au moment de la vente.
Le GAM permet de répondre aux problématiques de sur-apprentissage (over-fitting) et sous-apprentissage (under-fitting) par définition optimale de la transformation de variable. Utilisant le maximum de vraisemblance restreinte (Restricted Maximum Likelihood, REML), le modèle définit de manière endogène la transformation optimale de variable à adopter. 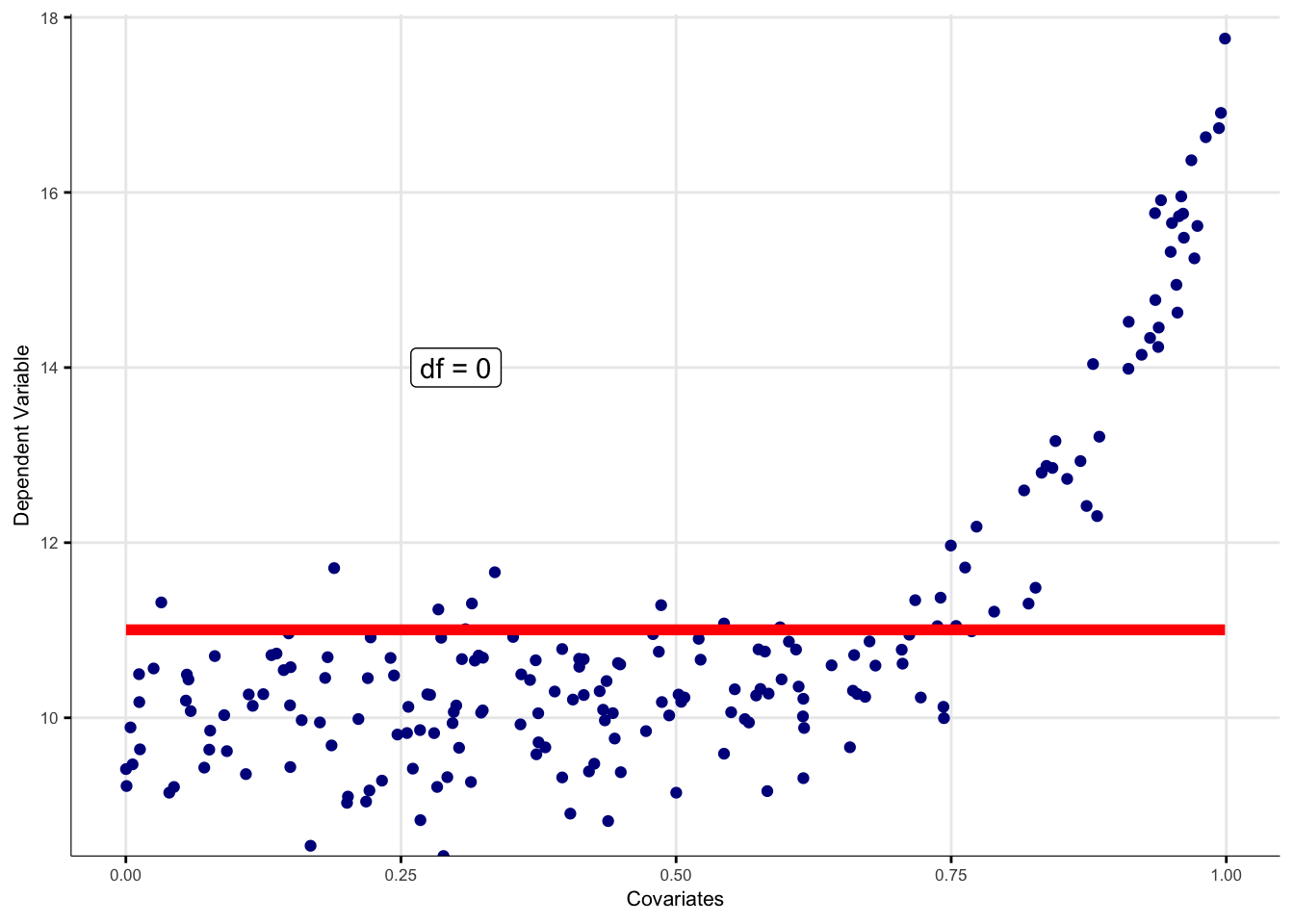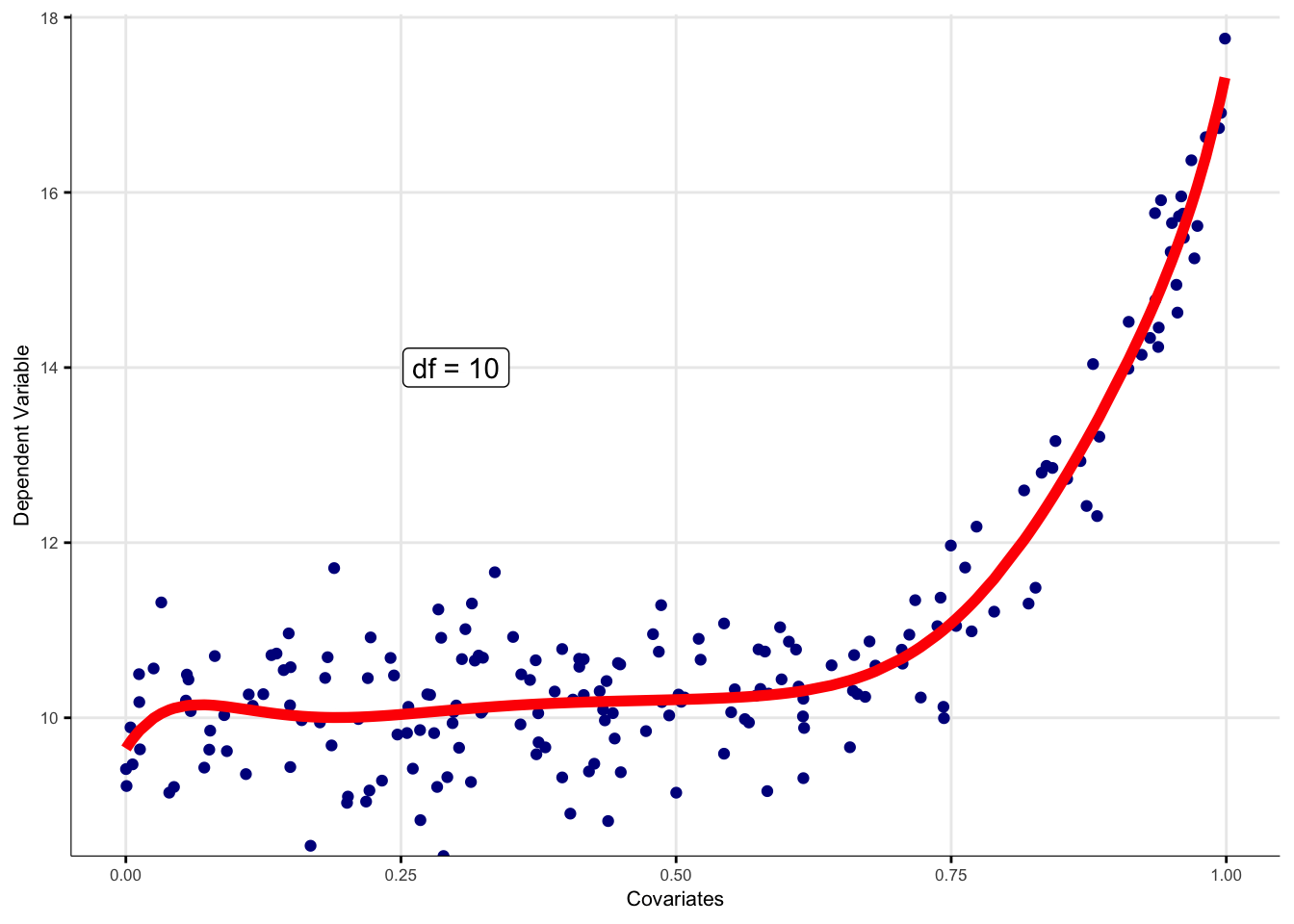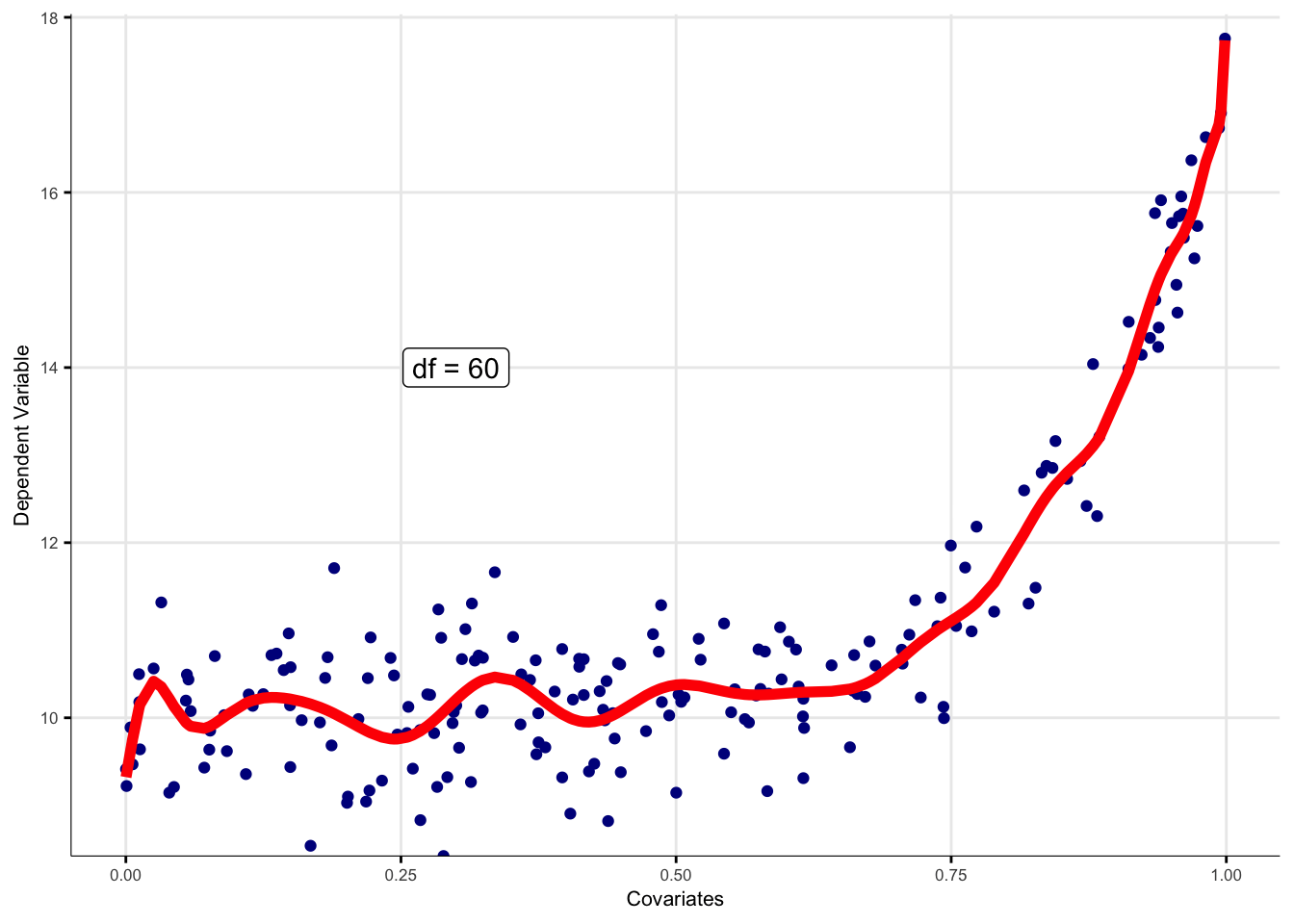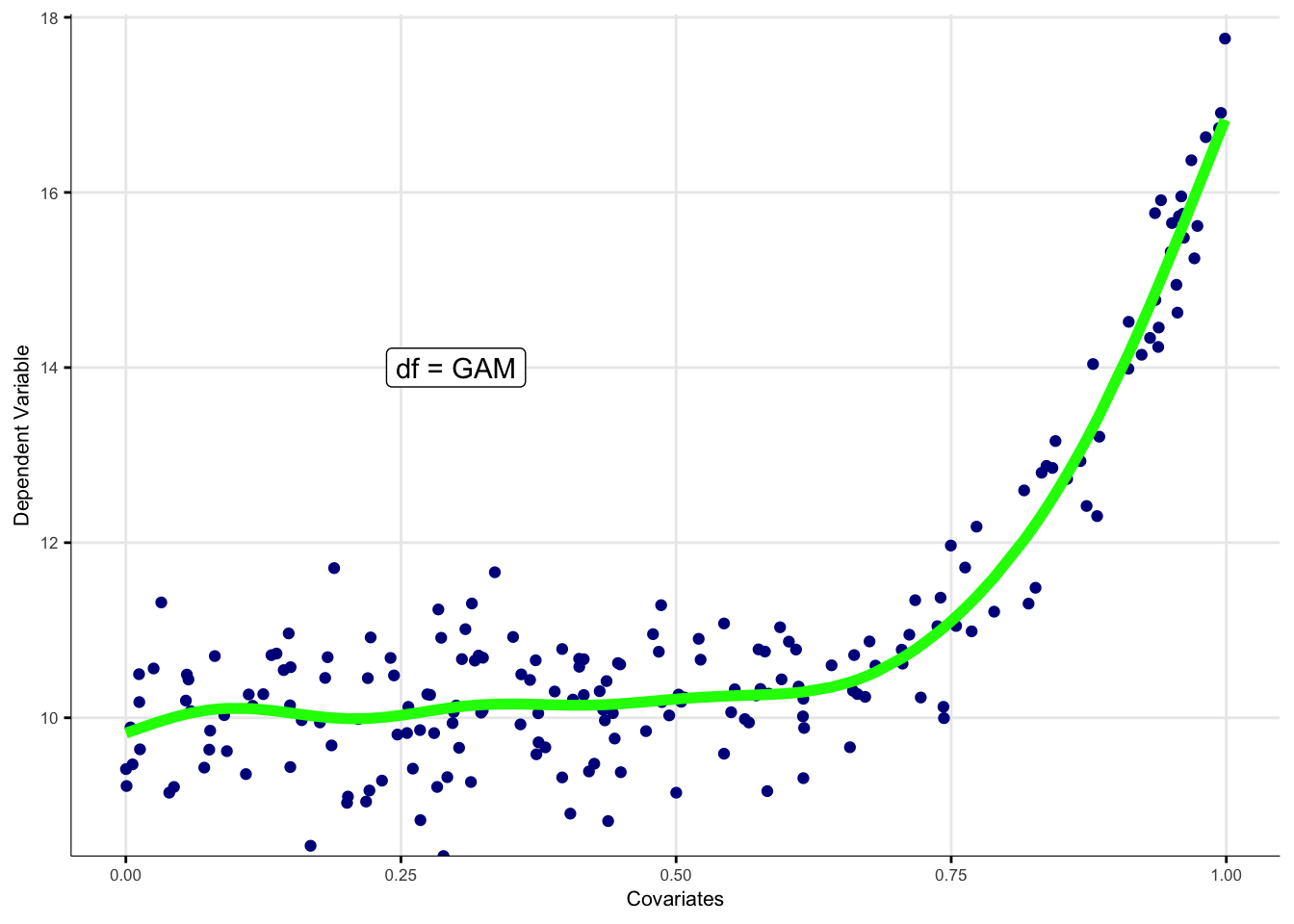L’opérateur doit spécifier les baseline smooth, classes de fonctions pour transformer la variable en question. Dans le cas où le degré de liberté est fixé à 1, alors la transformation de variable appliquée est une transformation linéaire. Dans le cas où la valeur est fixée à 0, alors la transformation appliquée est la moyenne des observations.
Nous illustrons le principe général de la transformation de variable avec le cas suivant.
Dans ce cas, la fonction génératrice est une puissance 7. Lorsque df = 0, la valeur estimée
est bien la valeur
moyenne, alors qu’une augmentation de df permet de réduire le sous-apprentissage
(underfit). À l’inverse, une valeur
trop
importante aboutit à un phénomène de sur-apprentissage (overfitting). La prédiction issue du GAM
permet un bon
compromis
entre l’overfit et l’underfit. Notre modèle de prix exploite ce processus de
transformation de variables pour les variables retenues
dans la définition du modèle de prix.
En outre, le même procédé est appliqué pour les coordonnées spatiales, mais la transformation de variables est une transformation bi-variée, permettant de traiter l’interaction entre longitude et latitude. Dans le cas du modèle de prix présenté, l’interaction est même triple, car la dimension spatiale interagit avec la dimension temporelle pour permettre une croissance hétérogène dans l’espace des valeurs immobilières.
Dans le cas bi-varié (pour une année donnée par exemple), un plan est renvoyé. Ce plan représente la déviation par rapport à la valeur moyenne, à caractéristiques équivalentes. Nous reportons ci-dessous le plan obtenu pour la dépendance spatiale avec un modèle de prix restreint à la commune de Paris. Le modèle estimé est un modèle simple avec comme variable de contrôle la surface du bien.
De plus, dans un modèle unique, il est possible d’estimer une dépendance spatiale par catégorie (par exemple type de biens), mais nous ne retenons pas ce choix.
Le modèle retenu exploite donc la surface du bien, la surface des dépendances associées au logement, ainsi que l’âge du bâti à l’instant de la transaction. Les transformations de variables sont réalisées pour chaque type de logement. En outre, les coordonnées spatiales sont ajoutées, en interaction avec la dimension temporelle. L’estimation est réalisée au 1er janvier de chaque année. Les paramètres retenus (maximum degree of freedom) pour les transformations de variables sont :
Comme la dimension spatiale est centrale dans le modèle de prix, il est impératif d’ajouter les opérations frontières aux zones d’emploi afin de ne pas introduire des effets de bord. Dans notre cas, on ajoute les opérations qui sont dans une zone de 5 km de la frontière de la zone d’emploi. Il faut retenir que plus la fonction de lissage spatiale est fine (donc degré de liberté élevé), plus le rayon nécessaire pour supprimer les effets de bord est réduit.
On affiche la différence de prédictions pour les opérations proches de la frontière de la zone d’emploi selon les deux scénarios (restreint aux observations de la zone d’emploi / ajout des opérations proches).
On remarque que la prédiction générale n’est pas affectée, sauf pour les observations proches de la frontière. On supprime donc les effets de bord en procédant de la sorte.
Le modèle de prix construit se base sur les caractéristiques des observations, en incluant une fonction de lissage spatio-temporelle permettant de capter des effets spatiaux cross-sectional, mais aussi de permettre une croissance des prix hétérogène dans l’espace.